Back to my personal projects page

pysimscale

Large scale similarity calculations with support for:

• Thresholds & sparse representations of the similarity matrix (using sparse API from Scipy package)

• Parallel of calculations, using the Joblib package.

• Quotient / Hierarchical similarity calculations, for cases where you want to group or aggregate the similarity graph to calculate similarity between higher level entities. For example similarity between users (higher level entity) derived from similarity between user reviews.

Background

A smart dev-ops engineer once told me:

Before I give you a cluster, show me you can fully utilise a single machine

With that in mind I created this package to share my experiences working on large scale similarity projects. One of the main problems I’ve encountered was scaling up similarity calculations and representation. Specifically how to better distribute calculations (focus on utilising a single, multi-core machine as efficiently as possible) and efficiently store the result, especially when low values are not very interesting (making the similarity matrix very sparse)

This package contains tools for handling this kind of the above problems.

Assumptions

• Data is numeric (binary, integers or real numbers). For categorical data please convert first (embedding, 1-hot encoding or other methods)

• The NxM matrix of features (N rows, M features) can be contained in memory and can expose a Numpy array API.

Installation

git clone git clone git://github.com/ytoren/pysimscale.git

Usage

Similarity calculations

• To enable parallel calculations please install the joblib package (it is not a dependency)

• Built-in, fully parallel support is available for Cosine and Hamming similarities. You can specify your own similarity function as long as it supports a “single row against the entire matrix” kind of output.

Example: cosine similarity

a = array([[1, 1, 1, 1], [0, 1, 0, 2],[2.2, 2, 2.2, 0.5]])

To return the full similarity matrix (no thresholding using a simple loop over the rows):

sim = truncated_sparse_similarity(a1, metric='cosine', thresh=0, diag_value=None, n_jobs=1)
print(sim.todense())

More practically, we don’t care about low similarity values (let’s say <0.9) so we can use a sparse representation. We also don’t need a diagonal of 1s (save some memory)

sim = truncated_sparse_similarity(a1, metric='cosine', thresh=0.0, diag_value=0, n_jobs=1)
print(sim.todense())

Now let’s do it in parallel! If we want to optimise the use of a single machine in our cluster we can send bigger “blocks” to the workers (instead of calculating 1 row at a time) using the block_size parameter.

sim = truncated_sparse_similarity(a1, block_size = 2, metric='cosine', thresh=0.0, diag_value=0, n_jobs=-1)
print(sim.todense())

Parallel calculations

The package used for cluster computing is joblib, but it is not a dependency by design. When joblib is installed, the function will default to parallel calculations (n_jobs=-1). However, if the package is not installed then the function will fall back to simple loops, even if you try to force it through the n_jobs parameter (this is designed to allow deployment in less-than-ideal cluster environments)

Quotient similarity

Let’s assume we calculated similarity between a set of text embeddings (say using TF-IDF and cosine similarity) and now we want to “aggregate” those links to calculate similarity between a higher-level entity like “users”. We assume we have the one-to-many link user -> texts. By grouping all the rows/columns that belong to the same higher-level entity we can derive higher-level similarity matrix [ref TBD]. We use a “list-of-lists” approach: each higher-level entity is represented as a list of indices from the original matrix, so that in total we have a proper partition of the sorted matrix:

m_users = quotient_similarity(m, partition, agg='sum')

The parameter agg is used to decide how we aggregate the values of the original matrix into the higher level matrix (see documentation for the available options).

“One is enough” similarity

If a single connection between the lower-level entities is enough to link the higher level entities (e.g. one similar text is enough to link two users) you can work around a lot of the complexity of the calculations by using the original graph. The key notion is that all the messages that belong to the same user are somehow “similar”.

The level of that similarity and how it relates to the text similarity is an open questions, but you can use the function id_block_matrix to generate a block matrix with a give value (typically 1) that represents this prior knowledge. Combining this matrix with the text similarity matrix (for example adding and capping values at 1) creates a similarity matrix that can be used for downstream operations (like connected components, clustering, etc.) without the need to reduce the dimension of the problem.

Pandas tools

Similarly, Pandas is not a dependency for this package, but I did include some tools to handle series data. Specifically cases where each row contains a vector but some contain None/NAN/nan values. See print(series2array2D.__doc__) for details.

Benchmarks

Similarity

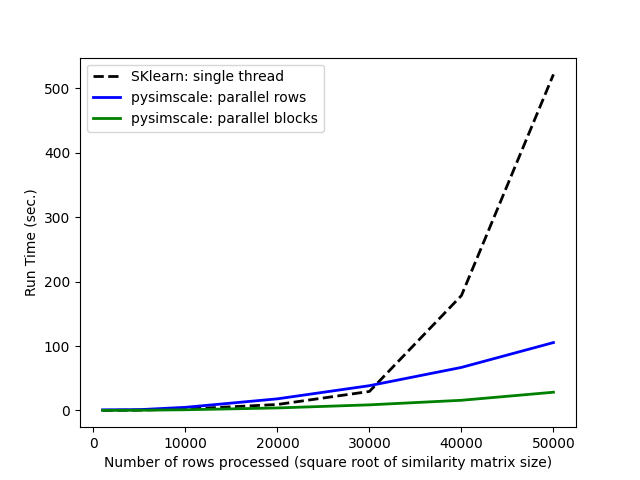
Comparing run times of the Scikit-learn cosine similarity function to our truncated_sparse_similarity function:

Code for simulation

Quotient Similarity

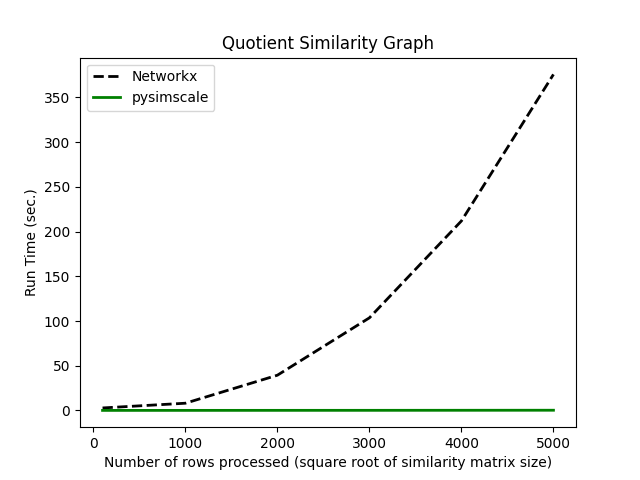
Comparing the run times of the Networkx quotient graph function to our quotient_similarity function:

Code for simulation